Segment Tree with Lazy Propagations

레이지 프로파게이션..배우겠다고 몇 번을 다짐한 자료 구조 중 하나이다. 

 

I. 단순 세그먼트 트리

 

우리가 처음에 구현한 세그먼트 트리는, 어떤 구간에 대한 연산과 특정 원소 ​하나​를 바꾸는 연산을 모두 O(logN)에 처리한다.

void update(ll n, ll k)
{
    n += base;
    IDT[n] += k;
    while (n > 1)
    {
        n /= 2;
        IDT[n] = IDT[n * 2] + IDT[n * 2 + 1];
    }
}
ll query(ll s, ll e, ll node, ll nodel, ll noder)
{
    if (noder<s || nodel>e) return 0;
    if (s <= nodel && noder <= e) return IDT[node];
    ll m = (nodel + noder) / 2;
    return query(s, e, node * 2, nodel, m) + query(s, e, node * 2 + 1, m + 1, noder);
}
​

 

단순한 세그먼트 트리의 코드는 대충 이렇다. 분석하자면..

 

1. 업데이트

 

​업데이트를 할 때는, 맨 아래 노드에서부터 시작해서 계속 자신의 부모에게 업데이트되는 숫자를 넘긴다.

따라서 시간복잡도는 트리의 높이에 의존한다.

트리의 맨 위 층은 1개 구간, 2층은 2개 구간, 3층은 4개, ..., (높이) 층은 base개 구간을 가지고 있으므로 세그먼트 트리의 높이는 O(log(base)) = O(log(N))이 됨을 알 수가 있다. 따라서 업데이트의 시간복잡도는 O(logN)이다.

 

2. 쿼리

 

​쿼리를 날릴 때, 세그먼트 트리는 각 층에서 2개 이하의 구간만을 사용한다. 

pf) 3개 쓴다고 하자. 구간끼리는 연속하므로 비둘기집 원리에 의해 한 방향에서 같은 층 쿼리가 연속한다. 그러면, 위 층으로 대체 가능하므로 모순

그래서 시간복잡도는 대충 O(2(높이)) = O(2logN) = O(logN)이 된다. 

 

대략 이런 자료구조인데, 이제 하고 싶은 걸 좀 바꿔 보자. 원래는 원소 ​하나​의 업데이트만 O(logN)에 지원했는데, 어떤 구간​ 업데이트를 O(logN)에 지원하게 하고 싶다. 그러면 어떻게 할까?

 

기존의 세그먼트 트리로 하면 O(NlogN)이 되어서 그냥 더하는 것 만도 못하게 된다. lazy propagation 기법은, 이 O(N)길이의 구간에 업데이트 하는 것 조차 O(logN)에 바로 뚫어버린다. 어떻게 하는 것인지 알아보자.

 

II. Segment Tree with Lazy Propagations

 

​이 기법을 내가 이해하기로는, 쿼리에 대응되는 모든 노드를 굳이 업데이트할 필요가 없이, 업데이트 한 것 처럼 '보이기만 하면' 된다는 것이다. 

이 '보이는 것'을 세그먼트 트리의 특징을 이용해서 효율적으로 구현한다.

 

당연히 이해가 안 갈 테니 그림으로 보자.

 

1. 구간 업데이트

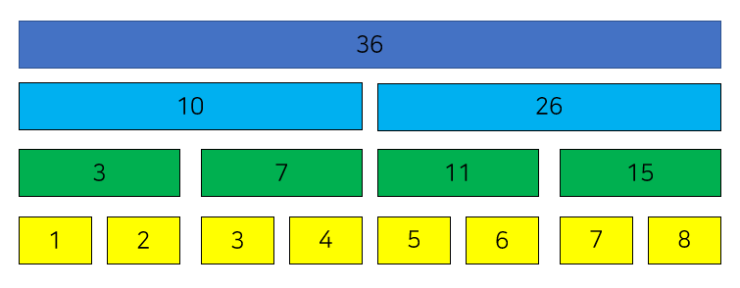
예를 들어, 위쪽 그림과 같은 세그먼트 트리를 생각해 볼 수가 있다. 이제 (1, 7) 구간에 2를 더하는 업데이트 쿼리를 날려 보자. 그런데, 일단 업데이트를 원래처럼 하지 말고, 일단 세그먼트 트리에서 (1, 7)구간에 구간 합 쿼리를 날릴 때 처럼 노드들을 분리해 보자.

빨간색으로 볼드 친 부분이 1~7까지의 구간 합을 구할 때 필요한 노드들이다. 우리는, 이제 저 곳에다가 일단 업데이트를 저장해 놓을 것이다. 즉, 업데이트를 당장 하지 않고 미래로 미룰 것이다. 왜 하필 저기에 저장하는지, 미룬다는 게 뭔지는 다음을 봐야 이해할 수 있으니 일단 그렇다고 하자.

 

이 미룬 업데이트는 각 노드마다 lazy라는 값으로 저장된다. lazy는, 이 노드에 붙어 있는 모든 리프 노드에 이 만큼씩을 더해야 한다는 뜻이다.

lazy까지 붙이고 난 뒤 세그먼트 트리는 이렇게 변한다.

좋다. 그러면 업데이트는 이대로 끝낸다. 미래의 내가 업데이트를 해 줄 것이고, 당장은 게으르게 미래로 미뤄 둔다. 업데이트 할 때 마치 쿼리를 구하듯이 O(logN)개의 노드에 접근하므로 업데이트 함수의 시간복잡도는 O(logN)이 된다.

 

2. 구간 합 쿼리

 

​​이번에는 구간 (2, 7)의 구간 합을 구하는 쿼리가 날아왔다고 해 보자. 그런데, 큰일이다! 우리는 실제로 업데이트는 하나도 안 해놨는데, 갑자기 맨 아래에 lazy조차 건들지 않은 2 노드가 필요하다. 하지만 걱정하지 않아도 된다. 

 

나 같이 게으른 사람은, 아무것도 안 해 놨을 때 이 두가지면 모든 걸 해결할 수 있다.

1. 몰아서 하기

2. 한 '척'만 대충 하기

 

놀랍게도 lazy propagation도 대충 그런 방식으로 동작한다. 백문이 불여일견, 빨리 계산해 보자.

 

 

구간 합을 계산하기 위해서 필요한 노드는 다음과 같다. 그런데, 이렇게만 보면 답이 없다. 탐색하는 과정에 대해서 생각해 보자.

 

저 초록색 '7' 노드에 도달하기 위해서는, 재귀적인 과정을 통해서 10을 일단 들러야 한다. 그런데, 10을 단순히 들르고 끝나는 것이 아니다. 탐색하는 과정에서, 방문하는 노드는 자신의 lazy값을 흡수 할 것이고(한 '척' 하기), 자신의 모든 자식 노드에 lazy값을 전파(Propagate)할 것이다(몰아서 하기). 그림으로 보자.

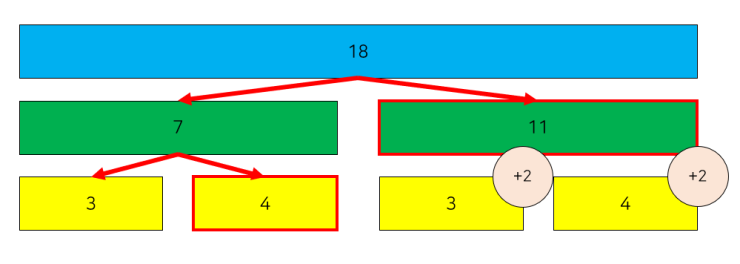
파란색 10과 그 아래 부분만 확대한 것이다. 현재 쿼리를 계산하기 위해 빨간색 화살표의 순서대로 탐색이 이루어진다.

현재는 파란색 10 노드를 보고 있다고 하자. 이제, 파란색 노드는 자신의 노드 값에 자신의 lazy 값인 2를 자신의 리프 노드 개수만큼 (즉, 업데이트 된 개수만큼) 더한다. 그 뒤 lazy를 초기화하고, 자식에게 전파한다.

 

이런 느낌? 그러면 이제 파란색 노드에는, 놀랍게도 리프 노드를 모두 갱신하였을 때의 값이 들어간다. 자신의 리프 노드에는 손도 안 댔으면서 말이다!! 이 행동을 재귀적으로 계속한다.

그 다음은 이럴 것이다. 그런데, 여기서 초록색 7(+2*2)는 자신의 자식을 더 이상 방문하지 않음에 살짝만 주목하고 넘어가자.

그 다음은 이럴 것이다. 리프 노드들은 자식이 없으므로 lazy를 전파하지 않는다. 또, 11의 경우에는 아까 전에 자식을 방문하지 않았기 때문에 그 자식들은 lazy값만 전파받고 끝이 났다.

최종적인 모습이다. 그런데, 이 알고리즘이 종료된 뒤에 리턴될 빨간색 테두리 노드들의 값을 보자. 모두 자기 자식들이 제대로 업데이트되었을 때의 값을 가지고 있다!! ​여기에서 lazy propagation의 진가가 드러난다. 쿼리에 필요한 빨간색 노드들만 당장 제대로 업데이트시킴으로서, 마치 내가 저 아래 리프 노드들까지 다 바꾼 것 처럼 보이게 해 놓는 것이다. 쿼리에 필요한 노드들의 개수는 해봤자 O(logN)개임을 위에서 보였고, lazy를 전파하는 행위는 시간 복잡도에 영향을 끼치지 않으므로(아마 상수 배일 것이다) query의 시간복잡도는 O(logN)으로 일정하다.

 

Wow!! 정말 아름답지 않은가? query를 수행할 때 일어나는 필연적인 탐색에, lazy라는 참신한 아이디어를 결합시켜서 더 복잡한 일들을 기존 세그먼트 트리와 같은 시간복잡도에 해결해 버렸다.

 

III. 구현

 

​​내가 배운 구현은 3가지 함수를 이용한다: lazy_update, range_update, 그리고 query. 이 부분은 독자가 재귀적 세그먼트 트리를 구현 할 줄 안다는 가정 하에 작성한다.

 

1. lazy_update( node, nodel , noder )

 

node의 lazy값을 적용하고, 자식들에게 전파하는 역할이다. node의 관할 범위가 [nodel, noder] 이다.

void lzupdate(ll node, ll nodel, ll noder)
{
    if (lz[node])
    {
        t[node] += (noder - nodel + 1) * lz[node];
        if (nodel != noder)
        {
            lz[node * 2] += lz[node];
            lz[node * 2 + 1] += lz[node];
        }
        lz[node] = 0;
    }
}

별로 안 맵죠? 그냥 lazy가 0이 아니면 흡수하고, 자손한테 전파한다. nodel == noder (즉, node가 관할하는 구역의 길이가 1) 이면 리프라는 뜻이므로 전파하지 않는다.

 

2. range_update( node, nodel , noder, s, e, k )

 

[s, e] 구간에 k를 더하는 업데이트를 하는 함수이다. 현재 방문한 노드의 번호가 node이며 관할 범위는 [nodel, noder]이다.

void rangeupdate(ll node, ll nodel, ll noder, ll s, ll e, ll k)
{
    lzupdate(node, nodel, noder);
    if (nodel > e || noder < s) return;
    if (s <= nodel && noder <= e)
    {
        t[node] += (noder - nodel + 1) * k;
        if (nodel != noder)
        {
            lz[node * 2] += k;
            lz[node * 2 + 1] += k;
        }
        return;
    }
    ll m = (nodel + noder) / 2;
    rangeupdate(node * 2, nodel, m, s, e, k);
    rangeupdate(node * 2 + 1, m + 1, noder, s, e, k);
    t[node] = t[node * 2] + t[node * 2 + 1];
}

i ) 남은 lazy값을 일단 전파

 

ii ) 만약 내가 쿼리를 구하는 노드에 포함된다면, 나에게 lazy값을 추가해줘야 함. ( 이 코드에서는 한 단계를 미리 나아간다 )

 

iii ) 포함되지 않는다면, 자식들도 방문.

 

iv ) 끝난 뒤 구간 합을 다시 계산해 준다. 근데, 사실 나는 위쪽에서 미리 해 놨기 때문에 계산을 다시 안 해도 상관없을 줄 알았는데 아니더라. ;;

 

3. query( node, nodel, noder, s, e )

ll query(ll node, ll nodel, ll noder, ll s, ll e)
{
    lzupdate(node, nodel, noder);
    if (nodel > e || noder < s) return 0;
    if (s <= nodel && noder <= e) return t[node];
    ll m = (nodel + noder) / 2;
    return query(node * 2, nodel, m, s, e) + query(node * 2 + 1, m + 1, noder, s, e);
}

간단하다. lazy 전파하고, 늘 하듯이 노드들을 가져간다. lzupdate에서 위에서 말한 행위를 해준다.

쿼리를 넣을 때는 query(1, 0, base-1, s, e)로 해주면 된다.

 

IV. 연습 문제 (난도순 정렬)

 

1. 레이지 감 잡기

 

백준 10999 구간 합 구하기 2

 

https://www.acmicpc.net/problem/10999

10999번: 구간 합 구하기 2

위에 구현해 놓은 걸 그냥 갖다 박으시면 해결 가능합니다.

 

풀이)

화이팅!

 

백준 17353 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별

 

https://www.acmicpc.net/problem/17353

17353번: 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별

레이지를 안 쓰고도 풀 수 있습니다. 레이지를 쓰는 것도, 쓰지 않는 것도 재밌으니 한 번 해보세요!

 

>> 풀이)

1. 레이지 쓰기

인접한 원소간의 차이를 생각해 봅시다.

1, 2, ..., R-L+1이라는 등차 수열을 구간에 더하기 때문에, 인접한 원소간의 차이는 1, 1, 1, ..., 1씩 늘어납니다.

그러면, 인접한 원소간의 차이를 lazy하게 업데이트하고, 차이들을 1번부터 구간 합 해주면 원하는 자리의 원소를 구할 수 있습니다.

여기서 양 끝 점만 주의해주시면 됩니다. R-L+1에서 갑자기 뚝 떨어질 테니까요.

 

2. 단순 세그먼트/펜윅만 쓰기

"나무 심기" 라는 문제와 거의 비슷합니다! 특정 점에 떨어지는 별의 수는, 쿼리의 시작점에서 떨어진 거리들의 합과 동일합니다. 단, 어떤 쿼리의 시작점부터의 거리가 R-L을 넘는 순간 그 쿼리는 영향을 주지 못하므로 세지 않습니다. 범위를 잘 조정해서 더합니다.

 

나무 심기 풀이 링크 >> https://blog.naver.com/insoo0327/222208708167

 

 

2. 레이지에 여러 가지 연산 합치기

 

 

보통 어려운 레이지 문제들은, 연산을 합치는 경우가 많습니다. 가령..

 

1. 구간 xor 업데이트 / 구간 합 쿼리

2. 구간 곱 업데이트 / 구간 합 쿼리

3. 구간 합 업데이트/ 구간 최솟값 쿼리

 

등등.. 정말 무궁무진합니다. 쿼리, 업데이트 뒤쪽에 원하는 함수를 아무거나 넣어보세요. 문제 하나가 뚝딱!

 

연산을 합치는 게 어려운 이유는, 연산간의 우선순위가 어렵거나, 리프 노드에 행한 연산이 부모 노드에 어떤 결과를 가져올지 모르기 때문입니다.

 

예를 들어, 구간 합 쿼리, 구간 덧셈 업데이트를 한다고 하면, 구간에 어떤 수를 덧셈하면 부모 노드에는 그 산하 노드 개수만큼 어떤 수가 더해집니다. 이 경우에는 노드간의 관계가 굉장히 명확해서 쉽게 구현 가능합니다.

 

하지만, 구간 합 쿼리를 하려는데 갑자기 구간 OR 업데이트가 들어온다고 생각해 보세요. 산하 노드들에 OR 연산을 했을 때, 구간 합이 어떻게 변할 지 예측할 수 있나요? 이렇게 되면 lzupdate 함수에서 t[node]에 대체 어떤 연산을 해야 제대로 된 값이 들어갈 지 알기가 힘듭니다.

 

이해가 되지 않으시더라도, 이건 직접 코딩을 하시다 보면 어? 하고 깨달으실 수 있을 겁니다.

 

레이지 프로파게이션의 작동 원리를 잘 이해한다면, 이런 문제들도 금방 해결하실 수 있습니다.

 

 

백준 1395 스위치

 

https://www.acmicpc.net/problem/1395

1395번: 스위치

이건 뭘까요.. XOR과 합? 조금 더 생각해보시면, 굉장히 효과적인 조합이 떠오를 겁니다.

 

>>  풀이)

구간 곱 업데이트와 구간 합 쿼리면 충분합니다. 꺼진 상태를 1, 켜진 상태를 -1로 놓고 해 봅시다.

간단한 계산을 해 주면 답을 구할 수 있습니다.

 

백준 17407 괄호 문자열과 쿼리

 

https://www.acmicpc.net/problem/17407

17407번: 괄호 문자열과 쿼리

왜 레이지가 필요한지를 생각해 낼 수 있다면 금방입니다.

 

>> 풀이)

왼쪽 괄호를 -1, 오른쪽 괄호를 1로 대응시킨 뒤, 괄호를 순서대로 더해나갈 때 그 합이 음수가 되지 않으면서 최종 값이 0이면 올바른 괄호 문자열이 됩니다.

(상당히 유명한 모델링입니다)

그러면 이제 다음과 같이 세그먼트 트리를 관리합니다:

 

1. 초기 괄호 값들을 저장

2. 세그먼트 트리의 i번째 인덱스에, 1~i번째 괄호값의 합 저장

3. 세그먼트 트리가 구간 최솟값 쿼리를 지원하게 하고, 만약 구간 최솟값이 음수면 올바른 괄호 문자열이 아니므로 NO 출력

+ 포인트 쿼리를 통해 총합이 0인지 체크

4. 세그먼트 트리가 구간 덧셈 업데이트를 지원하게 하고, 괄호 값이 바뀔 때마다 변화하는 구간합들에 적절한 수 더하기

ex)          (  (  (  (   )   )   )   (    )

괄호값     1 1 1 1 -1 -1 -1  1 -1

세그        1 2 3 4   3  2  1  2  1

 

3번째 괄호를 )로 바꾼다 -> 괄호값이 1에서 -1로 바뀐다 -> 뒤쪽 구간합들이 모두 2 감소

 

최솟값과 덧셈은 한 번 생각해 보시길 바랍니다. 수식으로 표현해 보셔도 재밌습니다. 

레이지가 통하는 함수들의 형태를 대강 느낄 수 있습니다.

 

백준 13925 수열과 쿼리 13

 

https://www.acmicpc.net/problem/13925

13925번: 수열과 쿼리 13

이번에는 두 가지를 lazy하게 전파해야 합니다. 심지어 원소들도 바꿔야 하네요. 안타깝게도 곱셈과 덧셈은 순서가 존재합니다.

 

>> 풀이)

일단 레이지 배열을 두 개 놓아야겠죠?

 

1. 같은 노드에서 순서 관계

무조건 곱셈을 전파한 다음에 덧셈을 전파하는 것으로 하겠습니다. 그러면, 쿼리를 ax+b꼴로 처리하면 됩니다.

덧셈을 전파하고 곱셈을 전파하는 거..는 할 수는 있을 것 같습니다.

 

2. 다른 노드에서 레이지가 전파되어 올 때

아마 여기서 많이들 절으셨을 것 같습니다. 두 레이지를 어떻게 합성할까요?

현재 노드에 ax+b 쿼리가 걸려있다고 하겠습니다. 이 상태에서 d를 곱하고 c를 더하는 레이지가 전파되었다면,

저 노드의 쿼리는 d(ax+b)+c가 되고 이는 곧 adx+bd+c가 됩니다.

그러면 이제 ad를 곱하고 bd+c를 더하는 쿼리로 합성됩니다. 이걸 lzupdate 내에서 구현해 주시면 됩니다.

 

3. Ai = V

전 이걸 며칠만에 깨닫고 PS를 접을까도 고민했습니다.

V = 0*Ai + V입니다.

 

백준 12858 Range GCD

 

https://www.acmicpc.net/problem/12858

12858번: Range GCD

업데이트 쿼리는 평범한 구간 더하기인데... GCD요?? 

수학을 잘 하신다면 구현은 앞 문제보다 월등히 쉬울 겁니다.

 

>> 풀이)

하나의 관찰이면 충분합니다.

$gcd\,(a, b, c, d, ...) = gcd\,(a, b-a\,, c-b\,, d-c\,, ...)$

 

증명은 수학적 귀납법으로 가능합니다. 힌트는 $a|b$이고 $b|a$면 $a=b$라는 것입니다.

 

이걸 아신 뒤에는 차이로 접근하시면 풀 수 있습니다. 세그먼트 트리와 레이지 세그먼트 트리, 두 개가 필요할 겁니다.

쿼리를 따로 처리하게 되거든요.